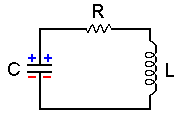
Figura A5.1 – Circuito RLC
Aula-5
Circuito RLC
Circuito RLC com fonte
Ressonância
em Circuitos de Corrente Alternada
Potência
em RLC com fonte
Examinaremos agora, um circuito contendo três elementos em série, um resistor R, um indutor L e um capacitor C, veja fig. A5.1. Seja VR , VL e VC as voltagens para cada um desses elementos, em um dado instante.

Figura A5.1 – Circuito RLC
Usando a segunda lei de Kirchhoff, podemos construir a equação diferencial que descreve a evolução temporal dos elementos deste circuito. Assumimos que o circuito não tem fonte externa e que o capacitor tenha sido carregado previamente. Assim,
![]() (A5.1)
(A5.1)
Sendo i = dq/dt, por definição de corrente elétrica, teremos:
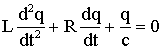 .
(A5.2)
.
(A5.2)
(A5.2) é uma equação diferencial de segunda ordem, completa e homogênea.
No caso do circuito LC, estudado na seção anterior, mostramos que o sistema oscila indefinidamente pois não tem resistência elétrica para dissipar calor. O circuito RLC da fig. (A5.1) difere do caso anterior pela existência do resistor R. Isto significa que haverá perdas de energia em forma de calor.
As soluções da equação diferencial (A5.2) devem ser de forma tal que descreva o comportamento de um circuito oscilante amortecido.
Uma possível solução da eq. (A5.2) será dada por:
![]() (A5.3)
(A5.3)
Cujas condições de contorno usadas são, t = 0 Þ q = qo = Ao . Neste caso, como a carga do capacitor tende a zero com o passar do tempo, a amplitude deve refletir o mesmo comportamento.
Para verificar em que condições a eq. (A5.3) é solução da equação diferencial, substituiremos (A5.3) em (A5.2). Isto é,
![]() (A5.4a)
(A5.4a)
e
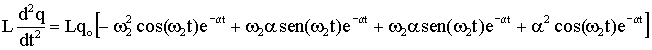 (A5.4b)
(A5.4b)Substituindo os dois últimos resultados na equação
diferencial (A5.2) temos que;
![]() +
+
![]() = 0
(A5.5)
= 0
(A5.5)
Simplificando temos que,
![]() (A5.6)
(A5.6)
Esta equação só será nula para qualquer instante t, se e somente se ;
![]() (A5.7)
(A5.7)
Este sistema de equações tem a e w2 como incógnitas. Resolvendo o sistema acima obtemos ;
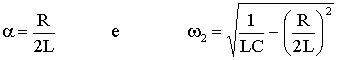 (A5.8)
(A5.8)
Usando os resultados acima escreveremos a equação que descreve a variação da carga em função do tempo;
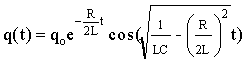 (A5.9)
(A5.9)
Como podemos observar, a carga no capacitor é oscilante e decresce com o tempo de uma forma exponencial.
A simulação abaixo mostra o funcionamento de um circuito RLC. Observe que, neste caso, o circuito não oscila indefinidamente, como no caso LC. No caso RLC a presença da resistência R (lâmpada) consome a energia inicialmente armazenada no capacitor. Veja que a energia total EE + EB vai diminuindo com o tempo. ED é a energia dissipada na resistência (lâmpada). Tanto a carga q(t)quanto a corrente i(t) são decrescente no tempo.
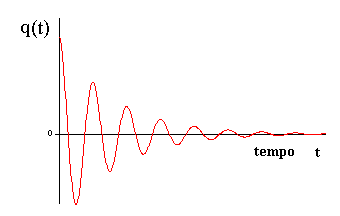
Fig. A5.2 - Carga no capacitor em função
do tempo
Para compensar a perda de energia do circuito RLC, anterior, podemos introduzir uma fonte que seja variável no tempo. Assim, a energia perdida no resistor vai ser compensada pela energia externa adicional cedida pela fonte. Um circuito elétrico com estas características é representado na figura (A5.2).
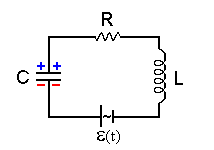
Figura A5.3 -Circuito RLC com fonte externa
de corrente alternada externa.
Assumimos que a fonte externa oscila com uma freqüência angular w como;
![]() (A5.10)
(A5.10)
Aplicando a segunda lei de Kirchhoff, como no caso do circuito RLC, teremos;
![]() (A5.11)
(A5.11)
ou
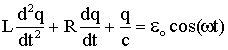 (A5.12)
(A5.12) A equação diferencial acima é
de segunda ordem, completa e não homogênea. Uma análise
física do novo sistema leva-nos a concluir que o sistema oscilará
indefinidamente, pois, as perdas de energia promovidas pelo resistor serão
compensadas pela fonte externa. Desta forma, uma solução
para a equação diferencial acima deve ser do tipo senoidal.
Levando em conta as afirmativas acima, suporemos
que a carga no capacitor seja uma função oscilante, dada
por,
![]() (A5.13)
(A5.13)
sendo qo a carga máxima no capacitor, w a freqüência angular do circuito e f a fase.
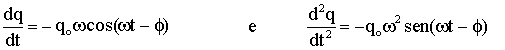 (A5.14)
(A5.14)
De onde tiramos que a corrente no circuito será igual a,
![]() .
(A5.15)
.
(A5.15)
Substituindo estes resultados na equação diferencial (A5.12), temos que,
![]() (A5.16)
(A5.16)
ou, de uma forma mais simplificada,
![]() .
(A5.17)
.
(A5.17)
Usando as identidades trigonométricas :
![]() (A5.18)
(A5.18)
![]() (A5.19)
(A5.19)
Temos que,
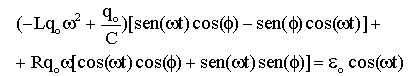 (A5.20)
(A5.20)reorganizando os coeficientes de cos(w t) e sen(w t) obtemos,
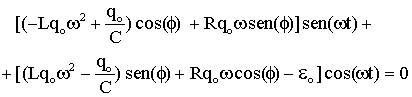 (A5.21)
(A5.21)
Esta equação deve ser satisfeita para todos os instantes t. Isto somente ocorrerá quando os coeficientes dos termos cos(w t) e sen(w t) forem todos nulos simultaneamente.
O coeficiente do sen(w t) leva-nos a seguinte relação,
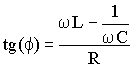 (A5.22)
(A5.22)
Na figura abaixo mostra o "triângulo de impedância",
de onde podemos tirar os valores do cos(f )
e sen(f ).
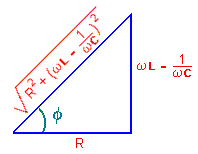
Fig. A5.4 – Triângulo de impedância
Substituindo os valores de cos(f ) e sen(f ) no coeficiente do termo cos(w t) da equação (A5.21) temos que,
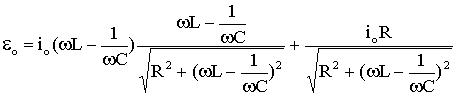 .
(A5.23)
.
(A5.23)
Dessa equação, podemos definir a corrente efetiva no circuito através de,
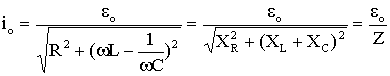 .
(A5.24)
.
(A5.24)
Z
® impedância
XL
® reatância indutiva
XC
® reatância capacitiva
X = XL + XC
® reatância
Devemos notar que a maioria das grandezas descritas acima, são dependentes da freqüência w. Como conseqüência, a amplitude de corrente io também dependerá de w.
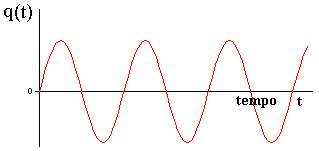
Figura A5-5 -Carga no capacitor em função
do
tempo para um circuito RLC.
A figura acima mostra que o capacitor é recarregado, pela
fonte externa, a cada ciclo.
3- Ressonância em Circuitos de Corrente Alternada
Nos circuitos RLC, com fontes alternadas, podem ocorrer o fenômeno denominado ressonância. Isto ocorrerá sempre que a freqüência angular da fonte externa for igual freqüência natural do circuito. Isto é, se XL e XC forem iguais em módulos, então temos que,
![]() (A5.25)
(A5.25)
Como conseqüência, a amplitude de corrente
io terá seu valor máximo quando a freqüência
angular da fonte assumir o valor acima.
A potência em um circuito RLC é dada por,
![]() .
(A5.26)
.
(A5.26)
A potência média no circuito pode ser obtida integrando P(t) num período de oscilação, como a seguir:
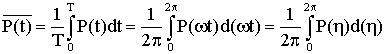 (A5.27)
(A5.27)
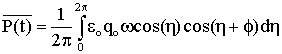 .
(A5.28)
.
(A5.28)
a integral acima pode ser escrita pôr;
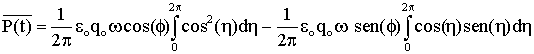 .
(A5.30)
.
(A5.30)
Resolvendo esta integral, encontramos a potência média do circuito, a qual é dada pôr,
![]() .
(A5.31)
.
(A5.31)
Na resolução da integral usamos o fato
de que o valor médio de sen2(w
t) é igual a ½ e que o valor médio de sen(w
t)cos(w t) é igual a zero.
![]() Voltar
à página principal
Voltar
à página principal
![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta página
está em constante atualização.
Sugestões serão bem-vindas.
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Dec/12/2000
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura