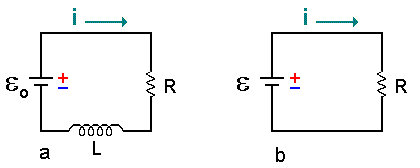
Figura A4-1 Circuito elétrico do tipo RL
Aula-4
Circuito RL
Energia Magnética
em RL
Circuito LC
Energia em LC
A seguir discutiremos o comportamento de um circuito elétrico contendo dois elementos: um resistor e um indutor, como mostra a figura A4-1.

Para encontrar as equações matemáticas que descrevem o comportamento deste tipo de circuito elétrico, faremos uso das Lei de Kirchhoff.

Kirchhoff
As quais podem ser enunciadas por;
- Lei dos Nós ou primeira lei de Kirchhoff:
A soma algébrica das correntes que fluem para qualquer nó ou junção de condutores ou circuitos é zero. Esta lei refere-se à conservação da carga. Como conseqüência podemos dizer que a soma das correntes que fluem para dentro de qualquer ponto de junção no circuito é igual a soma das correntes que fluem para fora daquele ponto.
- Lei da Malhas ou segunda lei de Kirchhoff:
A soma algébrica dos aumentos e quedas de tensão (potencial) através de qualquer malha fechada é zero. (Uma queda de tensão constitui um ganho negativo de tensão.) Esta lei é uma conseqüência da conservação da energia. Ela é simplesmente uma afirmação do fato de que o potencial elétrico pode ser estabelecido em qualquer ponto num circuito estacionário. Para um circuito fechado isto significa que,
![]()
A aplicação destas leis se dá considerando que, em cada ramo, existe uma única corrente dotada de um certo sentido. Ao se aplicar a lei das malhas, ocorre uma queda de tensão, ao se percorrer o resistor no mesmo sentido daquele escolhido para a corrente, e um ganho de tensão ao atravessar uma fonte de fem do pólo negativo (-) para o positivo (+). Se na solução ocorrer uma solução negativa para a corrente, isso quer dizer que a corrente real flui no sentido oposto àquele que se supôs.
Aplicando a segunda lei de Kirchhoff para os circuitos
apresentados na figura A4-1 temos;
![]() (A4.1)
(A4.1)
onde e1 é a força eletromotriz induzida no circuito. Lembramos que todos os circuitos elétricos contêm uma indutância assim como uma resistência elétrica própria.
A fem induzida e1 pode ser escrita em função da variação fluxo magnético ou da corrente real no circuito.
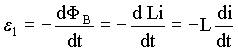 (A4.2)
(A4.2)
Substituindo a equação (A4.2) em (A4.1) encontramos uma equação diferencial para a corrente no circuito em função do tempo. (A4.3) é uma equação do tipo homogênea.
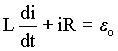 (A4.3)
(A4.3)
Existem várias técnicas para resolver (A4.3), isto é, determinar i em função do tempo. A seguir discutiremos uma delas.
Analisando a equação acima notamos que a função que descreve o comportamento da corrente i deve ser do tipo exponencial, pois a derivada dela é a própria função, a menos de constantes. Isto sugere-nos multiplicar ambos lados de (A4.3) por uma exponencial como a seguir;
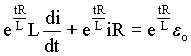 (A4.4a)
(A4.4a)
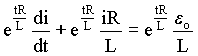 (A4.4b)
(A4.4b)
Os dois termos do lado esquerdo da equação (A4.4b) podem ser agrupados como a seguir;
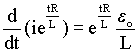 (A4.5)
(A4.5)
Integrando a equação acima temos que;
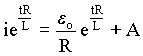 (A4.6)
(A4.6)
sendo A uma constante de integração, cujo valor pode ser determinado usando condições de contorno a partir de uma análise do circuito nos instantes iniciais. Neste caso assumimos que para o instante inicial, t = 0, a corrente no circuito é igual a zero. Isto implica no seguinte valor para a constante de integração A = -eo/R.
Substituindo na equação (A4.4) o valor encontrado para A temos que;
 (A4.7)
(A4.7)
onde iind refere-se à corrente induzida no circuito
e t = L/R a constante
tempo ou tempo característico do circuito.
O gráfico da figura A4.2 mostra o comportamento
da corrente em função do tempo dado pela equação
(A4.7).
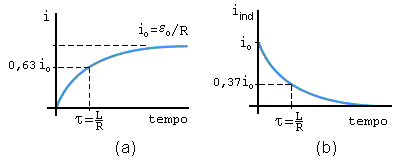
Figura A4-2
A corrente para t = t é igual a;
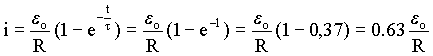 (A4.8)
(A4.8)
Isto significa que, a corrente do circuito é igual a 63% do valor máximo, quando t = t.
Observando a equação (A4.7) temos o
circuito terá inicialmente uma corrente variável no tempo
por um período muito curto, já que a iind é
proporcional a uma exponencial decrescente no tempo. Estes resultados levam-nos
a afirmar que, mesmo que a fonte geradora de correntes num circuito elétrico
é do tipo não variável no tempo, ela gera instantaneamente
correntes
induzidas.
A equação (A4.7) mostra-nos que a corrente será estabilizada para tempos relativamente grandes. Isto é, para t ® ¥ a i circuito será constante. Veja o gráfico na Fig.A4-2, representando o comportamento i com o tempo.
A força eletromotriz induzida pode ser determinada usando a equação A4.2,
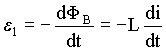 (A4.9)
(A4.9)
ou
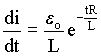 ou
ou 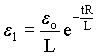 (A4.10)
(A4.10)isto mostra que a corrente induzida tende a zero para um tempo infinito, isto é
t ® ¥ Þ di/dt = 0 Þ e1 = 0
O gráfico (b) da fig.A4-2 mostra este comportamento.
O comportamento da energia magnética, criada no processo de indução, é armazenada no indutor. Procuremos responder algums questões básicas como,
- Como esta energia se comporta ?
- Ela é variável no tempo ou é
uma constante ?
- É possível encontrar uma equação
matemática que descreva o seu
comportamento, no caso do circuito RL
?
Na equação (A4.3) o primeiro termo corresponde a energia no indutor, o segundo termo corresponde a energia irradiada e o termo do lado direito da igualdade é a energia cedida ao sistema por uma fonte externa. Multiplicando ambos lado de (A4.3) obtemos uma equação para a potência, isto é;
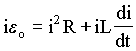 (A4.11)
(A4.11)
Por definição, a potência pode ser expressa em termos da taxa de variação da energia com o tempo, isto é
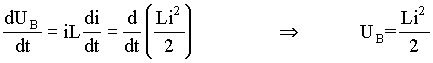 (A4.12)
(A4.12)
Onde UB é a energia magnética produzida
pelo indutor.
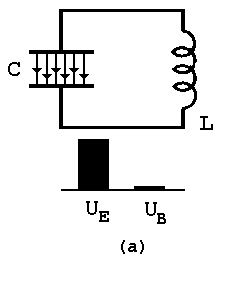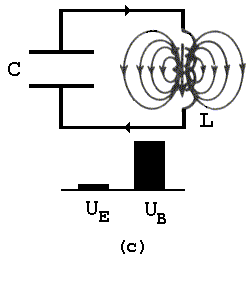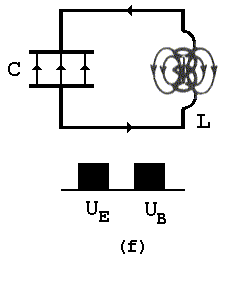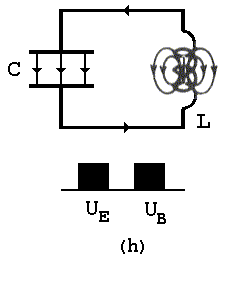
A figura abaixo mostra um circuito do tipo LC. No circuito (a), colocamos a fonte em contato apenas com o capacitor para carregá-lo. Após o carregamento completo do capacitor, desligamos a chave do ponto A e ligamos no ponto B desconectando a fonte do circuito. Mesmo assim o capacitor permanece carregado.
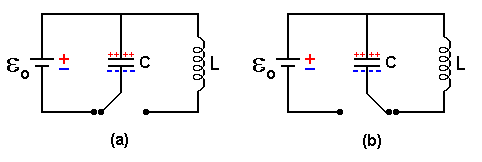
Figura A4-3
A ligação da chave no ponto B faz com que apareça uma corrente no circuito. Esta corrente passará pelo indutor criando consequentemente campos magnéticos. Isto significa que, parte da energia que estava armazenada no capacitor é transformada em energia magnética no indutor.
A seguir, mostraremos que é possível encontrar uma equação que descreva o comportamento temporal das cargas e correntes no novo circuito.
Existem vários métodos para resolver este problema. Um deles seria usar as leis de Kirchhoff como no caso anterior. Neste caso, diferentemente, determinaremos as equações para q e i usando a lei de conservação de energia, como a seguir.
Sabemos que as energias armazenadas num capacitor e num indutor são respectivamente dadas por;
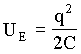 e
e 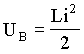 (A4.13)
(A4.13)
Como o sistema é fechado e ideal, temos que
a energia total (UT) no circuito é uma constante. Como
existem apenas dois elementos no circuito, podemos afirmar que a energia
total, deve ser uma soma das energias elétrica (UE) e
magnética (UB),
produzidas no capacitor e no indutor respectivamente. Assim temos que;
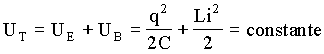 (A4.14)
(A4.14)
Derivando ambos lados da equação acima em função do tempo temos que;
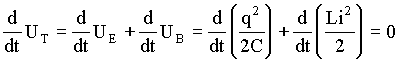 (A4.15)
(A4.15)
ou de uma forma mais simplifica;
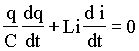 ou
ou 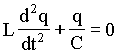 (A4.16)
(A4.16)
A equação acima é uma equação diferencial de segunda ordem, incompleta e homogênea. Como no caso anterior, existem vários métodos de resolve-la. Analisando a equação diferencial acima notamos que a derivada segunda de q(t) é a própria função q(t), a menos de algumas constantes. Isto sugere, intuitivamente, que a que a solução desta equação diferencial deve ser uma função do tipo seno, cosseno ou combinações delas. Com base nisto assumimos que q(t) em função do tempo seja da forma;
![]() (A4.17)
(A4.17)
onde A , w1 e f são constantes a serem determinadas, usando condições adicionais.
Inicialmente, como condição de contorno, assumimos que para o instante t = 0 a carga no capacitor é máxima, isto é q(t=0) = qo =A e a fase f = 0.
Substituindo esta equação para q(t) na equação diferencial acima, podemos facilmente verificar que q(t) é uma solução para (A4.16). Isto é;
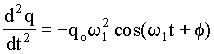 (A4.18)
(A4.18)
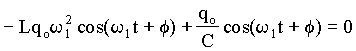 (A4.19)
(A4.19)Isto implica a constante w1 pode ser determinada. Neste caso podemos dividir ambos lados da equação por Lqocos(w1t + f ) o implica em;
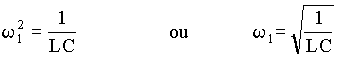 (A4.20)
(A4.20)
Observamos com isto que w1 deve ser a freqüência angular de oscilação do circuito.
A freqüência angular depende apenas da indutância e capacitância do circuito LC. Como a carga do circuito é variável no tempo consequentemente a corrente será também dependente do tempo.
Para verificar esta afirmação, basta derivar a equação (A4.17) em função de t. Isto é;
![]() (A4.21)
(A4.21)
A figura abaixo são os gráficos para a corrente e a carga variando no tempo.
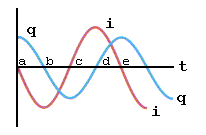
Figura A4-4
A energia total do sistema é a soma das energias elétricas e magnéticas, isto é;
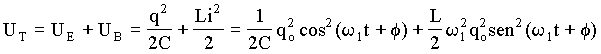 (A4.22)
(A4.22)
Substituindo (A4.20) e levando em conta que cos2(w1t+f ) + sen2(w1t+f ) = 1, temos que a energia total é realmente uma constante no tempo,
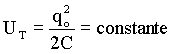 (A4.23)
(A4.23)
A energia total é exatamente igual a energia
cedida ao sistema, inicialmente, para carregar o capacitor. Analisando
os nossos resultados obtidos, concluímos que o circuito LC é
um circuito oscilante cuja freqüência natural é dada
por w1. w1
depende apenas das características do indutor (L) e do capacitor
(C). Como o circuito é ideal, isto é não tem resistência,
ele oscilará indefinidamente.
A figura abaixo esquematiza a evolução temporal de um circuito do tipo LC estudado aqui.
![]() Voltar
à página principal
Voltar
à página principal
![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta página
está em constante atualização.
Sugestões serão bem-vindas.
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Dez/12/2000
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura