Campos Escalares e Vetoriais
Operador Diferencial, Operações com
Teorema de Gauss, Teorema de Stokes
Aula – 7
Álgebra Vetorial, Diferencial
de uma Função
Campos Escalares e Vetoriais
Operador Diferencial, Operações
com![]()
Teorema de Gauss, Teorema
de Stokes
Revisão Matemática de Alguns Conceitos Básicos
Nesta seção apresentaremos alguns das principais propriedades da álgebra vetorial com o objetivo de introduzir o conceito de operador diferencial vetorial.
Considerando os vetores ![]() do R3, podemos definir as seguintes operações:
do R3, podemos definir as seguintes operações:
![]() - Produto escalar
- Produto escalar
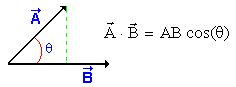
Fig.A7-1 -Projeção
do vetor A sobre B,
![]() - Produto de um escalar
por um vetor
- Produto de um escalar
por um vetor
![]() - Produto vetorial
- Produto vetorial
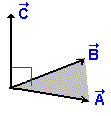
Fig.A-3 - Produto vetorial
![]() - Produto misto
- Produto misto
Em seguida, apresentamos algumas propriedades relacionadas
a diferencial de funções, que serão usadas durante
o curso.
Seja f uma função da forma,
![]() .
.
![]() ,
,
ou em termos de suas derivadas parciais,
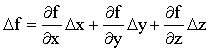 .
.![]() - Derivadas de segunda
ordem em f com relação à dois parâmetros independentes
x e y
- Derivadas de segunda
ordem em f com relação à dois parâmetros independentes
x e y
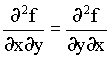 ,
,
isto significa que, os dois operadores diferenciais em x e y comutam.
![]() 3- Campos Escalares e Vetoriais
3- Campos Escalares e Vetoriais
Em física, é usual denominar-se por campo, uma grandeza dependente de um dado ponto no espaço e do tempo. Deste conceito define-se dois tipos de campos ; os escalares e os vetoriais.
![]() - Campos
escalares : São os campos que em um dado ponto do espaço
- Campos
escalares : São os campos que em um dado ponto do espaço
são descritos por um único
escalar. São exemplos de campos escalares;
a temperatura, o potencial elétrico,
o potencial gravitacional,…
![]() - Campos
vetoriais : São os campos que em um dado ponto do espaço
são
- Campos
vetoriais : São os campos que em um dado ponto do espaço
são
descritos por um conjunto de parâmetros
ou n-uplas. Para representá-los
por completo é necessário
conhecer o seu módulo e a sua direção. São
exemplos de campos vetoriais;
o campo elétrico, o campo magnético, o
campo gravitacional…
![]() 4- Operador Diferencial (gradiente)
4- Operador Diferencial (gradiente)
Utilizaremos o conhecimento sobre temperatura e condução
de calor para apresentar o operador diferencial, pela sua familiaridade.
Seja uma superfície, cuja temperatura varia
de um ponto para outro. Assumimos, por simplicidade, que ela decresça
de um ponto A para o ponto B, no plano. Veja figura abaixo,
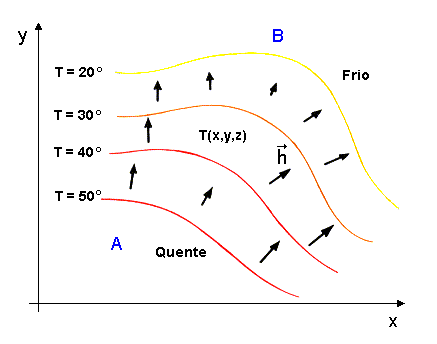
FigA7-4 -
Gradiente de temperatura e Fluxo de calor
Neste sentido, podemos dizer que existe um gradiente
de temperatura de A para B. Sabemos, também, que a temperatura é
um campo do tipo escalar. Mas, se existe gradiente de temperatura, isto
é, se a temperatura varia de um ponto para outro, então,
podemos falar de fluxo de calor. Fluxo de calor é uma grandeza vetorial,
pois para especificá-lo devemos conhecer a sua intensidade (módulo)
e a direção de propagação do calor.
Todos os comentários apresentados nesta
seção, continuam sendo válidos para qualquer campo
escalar usado, em particular o potencial elétrico. Neste caso, se
existe um gradiente de potencial ou diferença de potencial, entre
os
pontos A e B, então deve existir um campo vetorial associado
a isto. Este campo é o campo elétrico.
Em resumo, podemos dizer que a um campo escalar
tem sempre associado um campo vetorial. Vamos ver como estas relações
funcionam na prática.
Seja uma região do espaço onde a temperatura varia entre os pontos A e B. Assumimos, então que a temperatura seja função da posição no espaço R3. Isto é
Dessa forma a diferencial de T, ou a diferença de temperatura entre dois pontos é dada por,
![]()
ou
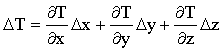
Podemos, agora rescrever o DT incluindo Dr da seguinte forma;
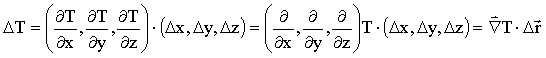
O resultado anterior mostra que a variação
da temperatura pode ser escrita em termos do gradiente da temperatura ![]() .
Isto implica que a partir de um campo escalar T=T(x, y, z) pode-se determinar
o campo vetorial associado, isto é
.
Isto implica que a partir de um campo escalar T=T(x, y, z) pode-se determinar
o campo vetorial associado, isto é
![]() .
.
De forma semelhante, pode-se proceder para encontrar uma relação entre o potencial e o campo elétrico. Isto é
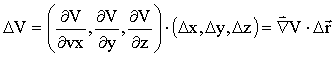
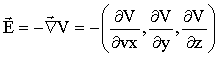 .
.
Temos, então, que o campo elétrico é proporcional
ao gradiente do potencial.
![]() - Produto escalar (operador
divergente)
- Produto escalar (operador
divergente)
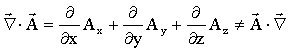
![]() - Produto de um escalar
pelo operador diferencial (operador gradiente)
- Produto de um escalar
pelo operador diferencial (operador gradiente)
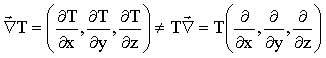
![]() - Produto vetorial (operador
rotacional)
- Produto vetorial (operador
rotacional)
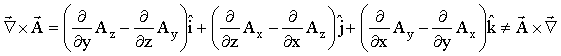
![]() - Produto misto
- Produto misto
![]() - Operador Laplaciano
- Operador Laplaciano
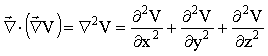
A seguir discutiremos sobre o teorema de Gauss o
qual está relacionado com a divergência de campos vetoriais.
Matematicamente, este teorema correlaciona uma integral de superfície
fechada com a integral do volume que esta superfície
delimita.

C. F. Gauss
Por motivos didáticos, usaremos um cubo infinitesimal como sendo o volume de integração. Em seguida, analisaremos o fluxo de um dado campo vetorial C sobre esta superfície. C pode ser qualquer campo vetorial, como por exemplo; o campo h que representa o calor que flui através de uma área unitária em uma unidade de tempo, ou mesmo o próprio campo elétrico que flui através da mesma superfície. Em suma, queremos dizer que as demonstrações são válidas para qualquer tipo de campo vetorial.
Consideremos o nosso cubo com arestas paralelas aos eixos ortogonais x, y e z, como mostra a figura abaixo.
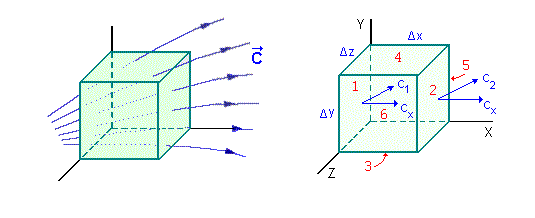
Fig. A7-5 - Fluxo de campo ventorial através de
uma superfície fechada
Assumindo que o cubo é infinitamente pequeno podemos dizer que, em primeira aproximação, uma variação no fluxo do campo pode ser escrito por;
![]()
O fluxo resultante que atravessa a superfície
do cubo pode ser determinado somando os fluxos sobre cada uma de suas faces,
como a seguir.
![]() - Fluxo que atravessa
a face 1
- Fluxo que atravessa
a face 1
![]() - Fluxo que atravessa
a face 2
- Fluxo que atravessa
a face 2
onde Cx(1) e Cx(2) são os valores do campo na face 1 e 2 respectivamente. Como as faces 1 e 2 são perpendiculares ao eixo x, por definição, temos que o fluxo resultante na direção x será a igual a diferença de linhas de campos que entra em 1 com as que saem em 2. Veja Fig.A7-5.
No caso geral DC numa dada direção é diferente de zero. Então temos que,
![]() .
.
Assim, o fluxo resultante na direção x (faces 1 e 2) será igual a,
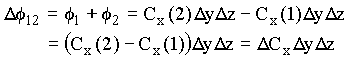
Substituindo na equação acima o valor de DCx podemos rescrever a equação para o fluxo resultante nas faces 1 e 2 como a seguir.
![]() - Fluxo resultante nas
faces 1 e 2, perpendiculares à direção x
- Fluxo resultante nas
faces 1 e 2, perpendiculares à direção x
![]()
onde DV é o elemento de volume, no caso o volume infinitesimal do cubo. Consequentemente, os Df resultantes para as faces 3-4 e 5-6, isto é nas direções y e z respectivamente, podem ser obtidos por analogia ao caso anterior. Isto é :
![]() - Fluxo resultante nas
faces 3 e 4, perpendiculares à direção y
- Fluxo resultante nas
faces 3 e 4, perpendiculares à direção y
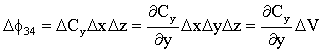
![]() - Fluxo resultante nas
faces 5 e 6, perpendiculares à direção z
- Fluxo resultante nas
faces 5 e 6, perpendiculares à direção z
![]()
O fluxo total do campo passando pelo cubo será uma soma das contribuições dos fluxos que atravessam (entram e saem) em todas as suas faces 1-2, 3-4 e 5-6. Assim,
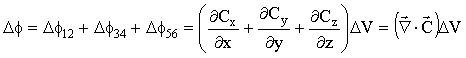 .
.
No caso de um volume infinitesimal, D V® 0, a equação acima pode ser rescrita da seguinte forma,
![]() .
.
Para obter o fluxo total, resultante, sobre o cubo basta integrar a equação acima no volume delimitado pela superfície escolhida, isto é
![]() .
.
Por outro lado sabemos que o fluxo de qualquer campo vetorial sobre uma superfície fechada dS, pode ser escrito em função de dS, isto é,
![]() .
.
Igualando as duas formas de calcular f , encontramos uma relação de suma importância entre uma integral de superfície fechada e uma integral no volume delimitado por esta superfície. Este resultado é conhecido como teorema de Gauss, o qual pode ser equacionado por,
![]()
ou numa outra notação por,
A seguir discutiremos sobre o teorema de Stokes o
qual está relacionado com o rotacional de campos vetoriais. Matematicamente,
este teorema correlaciona uma integral de caminho fechado com a integral
da área delimitada por este caminho.
Por motivos didáticos, usaremos no estudo
da circuitação um caminho quadrado infinitesimal. Em seguida,
calcularemos a integral de um campo vetorial C neste circuito fechado.
C pode ser qualquer campo vetorial, como por exemplo; o campo elétrico,
o campo magnético, o campo das velocidades da teoria dos fluidos,…
Em suma, queremos dizer que as demonstrações ou o teorema,
se aplica para qualquer tipo de campo vetorial.
Consideremos os nossos quadrados paralelos aos planos ortogonais (x,y), (x,z) e (y,z), como mostra a figura abaixo. Queremos agora encontrar a circuitação do campo C ao longo dos nossos pequenos quadrados. Será fácil calcular a integral de linha, se tomamos um quadrado suficientemente pequeno de forma que o vetor C não mude muito ao longo de qualquer lado do quadrado.
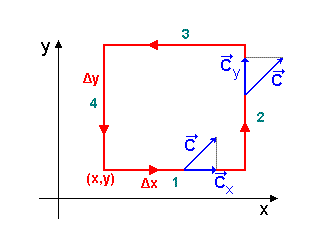
Seja a integral do campo C no caminho fechado, dado por,
![]()
No caso de um caminho infinitesimal esta expressão assume a forma,
![]()
Mas,
De forma análoga podemos construir os outros termos da soma acima. Assim,
![]()
Mas temos, por definição diferencial de uma função, que,
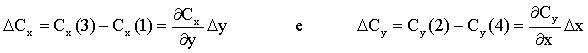
Substituindo estes resultados na equação para D wz, ela assume a seguinte forma,
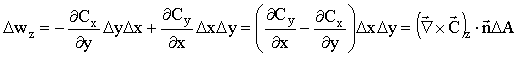
O termo entre parêntese corresponde à componente z do rotacional do vetor C. De forma análoga podemos calcular as integrais de caminho para as direções x e y, as quais são mostradas a seguir.
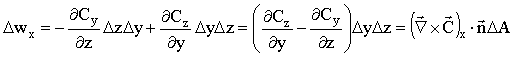
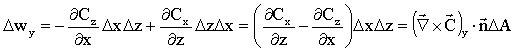 .
.
A integral de circuitação total será a soma das circuitações nas direções x, y e z. Isto é,
![]() .
.
No limite em que área delimitada pelos caminhos D A® 0 , D wassume a seguinte for diferencial,
![]() .
.
Integrando ambos lados da equação acima, temos que;
![]() .
.
Por outro lado sabemos que a integral de circuitação para qualquer campo em um caminho fechado é igual a;
![]() .
.
Igualando os dois resultados acima, encontramos uma relação de suma importância entre a integral de C em caminho fechado e a integral do rotacional de C sobre uma superfície aberta delimitado pelo caminho fechado dl. Este resultado é conhecido como teorema de Stokes, o qual pode ser equacionado por,

![]() Voltar
à página principal
Voltar
à página principal
![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta página
está em constante atualização.
Sugestões serão bem-vindas.
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Dec/12/2000
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura