Aula 14
O Conceito de Entropia
1)- A
Entropia e a Estatística
A idéia que
correlaciona desordem com entropia é melhor compreendida com o uso da
estatística ou análise probabilística. Este caso foi
primeiramente estudado por Ludwig Boltzmann (1844-1906).
Vamos tomar um exemplo prático analisando as possíveis combinações (cara e coroa) de um sistema com quatro (4) moedas. Denominaremos por estado cada uma destas combinações:
|
Macroestados |
Numero de estados possíveis |
No. de Microestado |
|
4 caras |
UUUU |
1 |
|
3 caras e 1 coroa |
UUUD, UUDU, UDUU, DUUU |
4 |
|
2 caras e 2 coroas |
UUDD, UDUD, UDDU, DUUD, DUDU, DDUU |
6 |
|
1 cara e 3 coroas |
UDDD, DUDD, DDUD, DDDU |
4 |
|
4 coroas |
DDDD |
1 |
Temos um total de 16
possibilidades ou 16 estados. Qual situação ou microestado
é a mais provável?
Nesta tabela, vemos que o
estado desorganizado (2 caras e 2 coroas) é o mais provável de
ser encontrado, a chance de encontra-lo nesta desorganização
é de 6/16.
2)- Outras
exemplos: Sistemas de Spins
O paramagnetismo, diamagnetismo
e o ferromagnetismo dos materiais podem ser entendido estudando o comportamento
e organização dos spin eletrônicos em um sistema
atômico e molecular.
-Já imaginou quantos
elétrons existem em um centímetro cúbico de ferro?
-Como calcular a desordem
de um sistema tão complexo como este?
-Tente aplicar o mesmo
procedimento usado no caso das moedas para calcular os possíveis estados
de organização dos spins (up ) (down ¯ ).
Vejamos para o caso de apenas 100 spins
|
|
¯ |
Numero de Microestados |
|
100 |
0 |
1 |
|
99 |
1 |
1,0 x 102 |
|
80 |
20 |
5,4 x 1020 |
|
60 |
40 |
1,4 x 1028 |
|
50 |
50 |
1,0 x 1029 |
|
40 |
60 |
1,0 x 102 |
|
20 |
80 |
5,4 x 1020 |
|
1 |
99 |
1,4 x 1028 |
|
0 |
100 |
1 |
3)- A Entropia de Boltzmann
Boltzmann (1844-1906)
propôs uma forma de calcular a entropia destes sistemas complexos.
Consideremos, por exemplo, dois sistemas moleculares A1, A2 os quais estão separados no estado de equilíbrio. Os macroestados de A1, A2 podem ser representados por
![]()
onde ni, Vi
e Ei são respectivamente os números de
partículas, volume e a energia de cada sistema.
|
A1 n1, V1, E1 |
A2 N2, V2, E2 |
O
número de microestados no sistema i é descrito por Zi(Ei),
conhecida como função partição.
![]() é o número de microestados possíveis em cada
sistema Ai
é o número de microestados possíveis em cada
sistema Ai
![]() número
de microestados dos sistema A1 + A2
número
de microestados dos sistema A1 + A2
Um dos passos importantes
na análise do comportamento desta função é buscar os
seus extremos (maximização ou minimização). Isto
é feito derivando Z em termos das energias envolvidas e igualando a
zero:
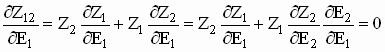 #9; no
equilíbrio
#9; no
equilíbrio
Como,
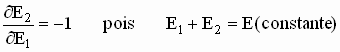
Então das duas
equações acima deduzimos que
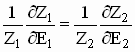
Esta equação
acima pode ser re-escrita por
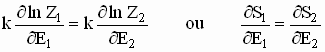
onde ![]() é
a Entropia de Boltzmann. Boltzmann mostrou ainda que a entropia estava
relacionada com a temperatura pela equação,
é
a Entropia de Boltzmann. Boltzmann mostrou ainda que a entropia estava
relacionada com a temperatura pela equação,
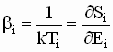
4)- Sobre
a Aditividade da Entropia - A Entropia é Aditiva ?
Se estamos tratando de dois
sistemas isolados, a propriedade de aditividade de qualquer conceito
físico é representado por uma soma direta dos conceitos, isto
é;
![]() número de partículas nos dois sistemas
número de partículas nos dois sistemas
![]() volume total dos sistemas 1 e 2
volume total dos sistemas 1 e 2
![]() Energia total
Energia total
Por definição
de entropia temos que a entropia do sistema composto é igual a;
![]()
![]()
Daí tiramos que a
entropia de Boltzmann é também é aditiva, isto é;
![]()
5)- Caso
Geral
O caso geral é
quando temos um número grande de sistemas interagentes e cada um destes
sistemas tem incontáveis micro-estados. Neste caso a entropia de
Boltzmann pode ser escrita por;
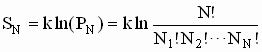
A probabilidade de se encontrar um estado qualquer Ni é dado por Ni /N= pi. Usando os resultados acima juntamente com a fórmula de Stirling
![]()
a entropia pode ser
re-escrita da seguinte forma,
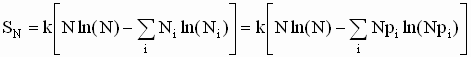
ou
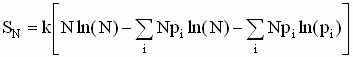
Levamos em conta,
também, que soma de todas as probabilidades tem que ser igual a um ou
normalizada, isto é,
![]()
Destas
equações tiramos que a entropia é igual a
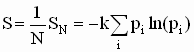
Conhecida também
como entropia de Shanon.
7)- Uma questão que podemos colocar
agora é:
a) Função
Partição
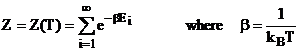
b) Energia Média
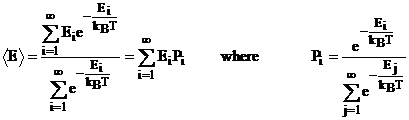
c) Entropia
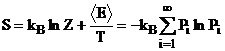
d) Energia Livre de Helmholtz
![]()
e) Dispersão
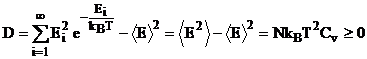
f) Calor Específico
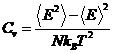
7)- Uma
questão que podemos colocar agora é:
É possível generalizar a entropia ?
Constantino Tsallis (1998)
propôs uma generalização da entropia postulando-a da
seguinte forma:
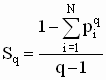
onde q é um
número real.
Mostraremos a seguir que as
entropias de Boltzmann e Shanon são casos particulares da Entropia de
Tsallis, no limite em que q ® , isto é;
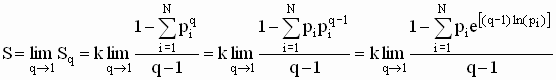
ou
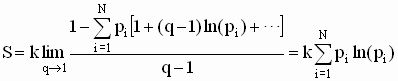
7)- Esta
entropia é aditiva ?
Pode se mostrar que esta
entropia não é aditiva, mas é pseudo aditiva, isto
é;
![]()
isto significa que a
entropia de Tsallis só é aditiva no limite em que q ® 1.
- isto é um
problema ?
- Existe
sistemas na natureza que comportam assim ?
- Um
prato cheio para um prêmio Nobel.