Aula-9
Transporte
de Energia em Ondas Eletromagnéticas
Vetor de
Poynting
Relação
Energia-Momento Linear
Aplicações
![]() 1- Transporte de Energia em Ondas Eletromagnéticas
1- Transporte de Energia em Ondas Eletromagnéticas
Nesta seção
discutiremos alguns conceitos e relações associados ao transporte
de energia em ondas eletromagnéticas. Este fenômeno é
de grande importância e tem sido usado em diferentes aplicações
tecnológicas, como o transporte de informações e de
energia de um ponto para o outro. O Sol, em particular, é uma grande
fonte de ondas eletromagnéticas e sua importância é
indiscutível em nosso dia a dia.
Introduziremos, a
seguir, a idéia de densidade de energia armazenada em campos elétricos
e magnéticos. Para isto, voltaremos às análises feitas
para o capacitor e indutor, em aulas anteriores.
Sabemos que
os capacitores e indutores são elementos em um circuito que têm
a propriedade de armazenar campo elétrico e magnético. Isto
significa que existe no interior do capacitor e do indutor energias armazenadas
eletromagnéticas. Encontraremos, em seguida, as expressões
que correlacionam as densidades volumétricas de energia armazenadas
nestes dois elementos.
Sabemos que a energia UC, em um capacitor pode ser escrita em função da capacitância C e da diferença de potencial entre as placas. Isto é,
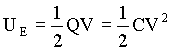 .
.No caso de capacitores de placas paralelas, cujas dimensões sejam muito maiores que sua separação, temos que o campo elétrico no seu interior é uniforme e está relacionado com a diferença de potencial entre as placas por V = Ed, sendo d a distância entre a placas. Por outro lado, temos que a capacitância pode ser expressa em função das características geométricas do capacitor, isto é, C = ÎoA/d. Substituindo estes resultados na equação para a energia temos que,
 .
.
Levando em conta que Ad é o volume do capacitor, podemos calcular a densidade de energia por unidade de volume (uE), no interior do capacitor ,dividindo ambos lados da equação acima pelo volume Ad,
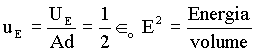
Procedendo de forma semelhante, podemos calcular a energia magnética armazenada em um indutor em função do campo magnético associado. Sabemos também, de aulas anteriores, que a energia magnética em um capacitor tem a forma:
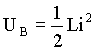 .
.
Temos ainda que a indutância pode ser expressas em termos das
propriedades geométricas do indutor, isto é, L = moN2A/d.
No caso solenóide, o campo magnético em seu interior é
igual a, B = moNi/d. Substituindo
estes dados na equação para a
energia magnética temos,
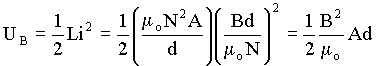 .
.
Consequentemente, a energia magnética por unidade de volume pode ser calculada dividindo ambos os lados da equação acima pelo volume do indutor (Ad). Assim
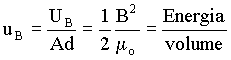 .
.
Podemos generalizar os resultados acima e dizer que as energias, por unidades de volume, armazenadas em campos elétricos e magnéticos são proporcionais ao quadrado das amplitudes dos campos E e B, isto é.
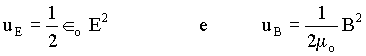 .
.
Então, para qualquer volume dado, a energia total armazenada em forma de campo elétrico e magnético é igual a integral das densidades de energias em todo volume,
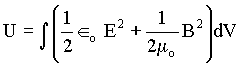
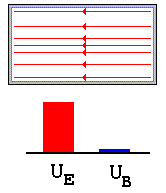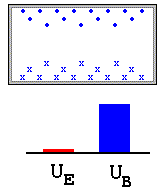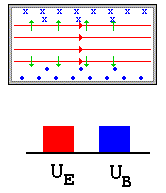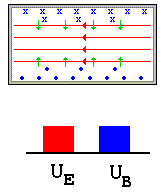
Uma conseqüência importante das equação Maxwell é o fenômeno relacionado à propagação de ondas eletromagnéticos. Das seções precedentes, vimos que a criação de campos elétricos e /ou magnéticos no espaço implicam no surgimento de energias armazenadas em forma de E e B.
Como as ondas eletromagnéticas se propagam pelo espaço arrastando os campos elétricos e magnéticos, então as energias associadas a estes campos devem se propagar pelo espaço de forma semelhante. Partindo deste pressuposto, podemos analisar o fluxo de energia eletromagnética, transportado através de um volume qualquer, definido por uma superfície gaussiana fechada. Isto é,
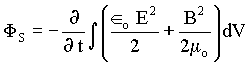 .
.Pelo teorema de Gauss, temos que uma dada integral de volume está sempre associada a uma integral superfície fechada. Isto é,
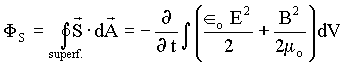 .
. Quando a energia
do campo está presente em forma de ondas eletromagnéticas,
ela pode ser carregada para dentro ou para fora da fronteira delimitada
por um volume. Este transporte é representado pelo vetor de Poynting,
S, cujo módulo é igual a energia propagada por unidade de
área na unidade de tempo. O sentido do vetor S estabelece o sentido
da propagação energia irradiada.
A seguir
determinaremos, explicitamente, a energia que é propagada pela onda
por unidade de área e unidade de tempo. Imaginemos para isto que
uma onda está atravessando uma área A perpendicular ao eixo
x, como mostra a Fig.A9-2.
Em um tempo Dt curto, a onda se move para a
direita em uma distância dx = c dt. A energia transportada nesse
elemento de volume é dada por,
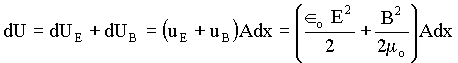 .
.
Sabemos que as amplitudes dos campos E e B estão relacionadas por, E = cB.
Substituindo este resultado na equação anterior temos que,
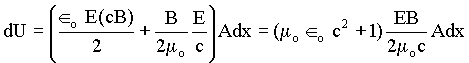 .
.
Como Îo mo c2 = 1, a equação acima pode ser escrita por,
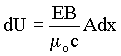 .
.
Essa é a quantidade de energia que atravessa a área a por unidade de tempo. Segue-se que o fluxo de energia por unidade de área e por unidade de tempo é igual a
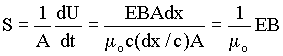 .
.Como e E e B são vetores, podemos rescrever o produto EB em sua forma vetorial,
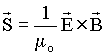 .
.
![]() -
A direção de S é a direção de propagação
da onda eletromagnética,
-
A direção de S é a direção de propagação
da onda eletromagnética,
![]() - O módulo
de S é proporcional a energia transportada pela onda.
- O módulo
de S é proporcional a energia transportada pela onda.
Assumindo que os campos elétricos e magnéticos têm a forma;
![]() ,
,
podemos calcular o valor médio do vetor de Poynting ou da energia média média transportada, por:
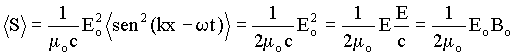 .
.
![]() 3 – Relação Energia-Momento Linear
3 – Relação Energia-Momento Linear
Uma partícula movendo-se em um meio resistivo sofrerá forças de oposição ao movimento. Em mecânica, esta forças denominadas de forças de atrito, são dependentes da velocidade de um dado corpo. Usando argumentos semelhantes ao da mecânica, vamos estudar as forças exercidas em superfícies condutoras, por uma radiação eletromagnética (EM).
Para entender este problema vamos analisar a interação de uma onda eletromagnética com um condutor. Isto é, analisaremos o choque de uma onda eletromagnética com uma placa condutora. Veja Fig.A9-3.
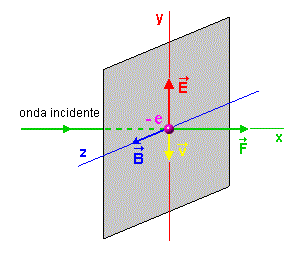
Fig.A9-3 - Uma onda luminosa inside sobre
uma placa condutora
O campo elétrico devido
a onda eletromagnética, ao interagir com os elétrons livres
do condutor, vai produzir uma força sobre eles do tipo F = eE. Esta
força fará com que os elétrons movam-se com um certa
velocidade v no interior do condutor, provocando assim o aparecimento de
pequenas correntes localizadas. Sabemos também, que adicionalmente
aparecerão forças magnéticas como conseqüência
do movimento dos elétrons na presença do campo magnético,
existente em uma onda eletromagnética. Assim as forças envolvidas
são do tipo;
![]() .
.
Por outro lado, sabemos que o movimento dos elétrons, no condutor, vai produzir uma força de atrito devido aos choques dos elétrons com as outras partículas na placa condutora. Estas forças de atrito ou de viscosidade, neste caso, são em geral proporcionais à velocidade da partícula no meio, isto é,
![]() ,
,
onde v é a velocidade dos elétrons e b é a constante de amortecimento. Comparando esta força com a força elétrica, podemos encontrar um relação para a velocidade do elétron em função do campo, isto é,
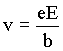 .
.
Substituindo esta velocidade na equação para a força magnética temos que
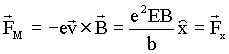 .
.
A força FM, sobre o elétron tem o sentido de x, sendo perpendicular ao plano formado pelos vetores v e B, isto é, ao plano yz. Veja Fig.A9-3.
De acordo com a segunda lei de Newton, Fx é igual a taxa de variação do momento linear com o tempo, isto é
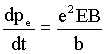 .
.
O momento linear é transmitido, a esta taxa, a todos os elétrons da lâmina e consequentemente à própria lamina. Isto significa uma força resultante não nula, empurrando a lâmina na direção x.
Resta, agora, relacionar a transferência de momento linear à com a absorção de energia pela a mesma. A componente elétrica da onda incidente realiza trabalho sobre cada elétron oscilante à taxa de
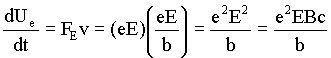 ,
,
onde temos usado a relação E = Bc . Note-se que a força
magnética Fx, sendo sempre ortogonal à velocidade
v, não realiza trabalho sobre o elétron oscilante.
![]() 4.a- Seja um condutor cilíndrico de comprimento h, raio a,
resistividade r, percorrido por uma corrente
i. Veja Fig.A9-4. Mostre que a potência
do fluxo de energia através da superfície do condutor, obtida
por integração do vetor de Poynting sobre essa superfície,
é igual à taxa de produção de energia térmica
por efeito Joule, isto é,
4.a- Seja um condutor cilíndrico de comprimento h, raio a,
resistividade r, percorrido por uma corrente
i. Veja Fig.A9-4. Mostre que a potência
do fluxo de energia através da superfície do condutor, obtida
por integração do vetor de Poynting sobre essa superfície,
é igual à taxa de produção de energia térmica
por efeito Joule, isto é,
![]()
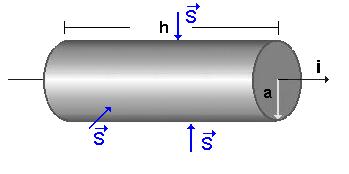
Fig.A9-4 – Cilindro condutor pecorrido
por uma corrente i
 .
.O campo magnético produzido pela corrente i pode ser calculado usando a lei de Ampère,
 .
.
Substituindo o valor encontrado para o campo B e assumindo que o diferença de potencial V = Ri, temos que
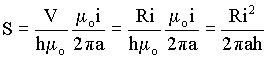 .
.
Levando em conta que A = 2pah é a área externa do cilindro, pode-se rescrever a equação acima como,
![]()
Mas, pela a figura acima (Fig.A9-4) temos que o vetor de Poynting a tem sentido oposto ao vetor normal à superfície do cilindro, assim
![]()
Comparando as duas equações acima temos que
![]()
![]() 4.b- Radiação Solar : A radiação eletromagnética
do sol que atinge a superfície terrestre é da ordem de 1350
J/m2seg. Calcule as amplitudes dos campos elétrico e
magnético transportado por esta onda eletromagnética.
4.b- Radiação Solar : A radiação eletromagnética
do sol que atinge a superfície terrestre é da ordem de 1350
J/m2seg. Calcule as amplitudes dos campos elétrico e
magnético transportado por esta onda eletromagnética.
Este problema deve ser calculado usando o valor médio do vetor de Poynting, dado por ,
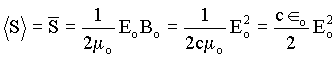 .
.
Assim o valor da amplitude do campo Eo é igual a,
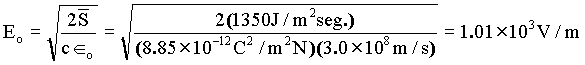
Calculamos agora a amplitude para o campo magnético, usando a relação Bo = Eo/c,

onde c é a velocidade da luz.
![]() Voltar
à página principal
Voltar
à página principal
![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta página
está em constante atualização.
Sugestões serão bem-vindas.
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Dec/12/2000
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura